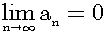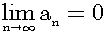The Integration of Mathematics

Summary

The Euclidean space is only in our brain. If we want to use Euclidean geometry in the real world, we need the minimum length.

Main Text

    The ancient Greeks considered that the base of all cognition is the natural number one. John Gabriel points out in "Euclid's point?" as following quotation: "The Greeks surmised there had to be a smallest particle of matter - they called this the atom. As the knowledge of science progressed, it was necessary to revise this model." Now, we cannot find indivisible atom, but the natural number one must be indivisible. Where does the natural number one come from?

   This question is difficult to answer, but Marcello Barbieri says in the organic codes as following quotation: "The great philosophers of antiquity discussed quite a number of world views, such as the atomic theory, determinism, relativity and evolution, and yet none of them conceived the cell theory, which makes us wonder why." The reason is as follows: "The answer is that the eye's retina itself is made of cells. Two objects can be seen apart only if their light rays fall on different cells of the retina, because if they strike the same cell the brain receives only one signal." Then, we need the microscope to find the cell. Marcello Barbieri says that the concept of the cell had to be imposed on us by the microscope because it was unthinkable in the world-view of classic philosophy. This is important point. Ancient Greeks considered that the matter consists of atoms. Now, this model must be revised. Instead, our cognition consists of units. The unit is the cell. Especially, the cell, which constitute the nervous system, is called the neuron. The neuron is the unit of our cognition.

   Mathematics has two origins: geometry and arithmetic. First, let us consider geometry. I say that the visual intelligence conceals the unit square from our consciousness: Area Is Essential for Euclidean Geometry. Then, the Euclidean space is only in our brain.

   Second, let us consider arithmetic. The basic subject of arithmetic is natural numbers. I say that a cell is the origin of the natural number one: What Is the Natural Number One? Additionally, I say that each DNA base has equality: Natural Selection Protects Information against Entropy. Moreover, natural selection strengthens the equality of each DNA base. Of course, because an important DNA base has nearly complete equality, the DNA base must also have indivisibility and invariability. Then, natural selection endowed each DNA base with properties of the natural number one: indivisibility, invariability, equality. In addition, we must not forget that natural selection is based on the indivisibility of a cell and the irreversibility of death of a living organism. So the cell is the origin of the natural number one. Therefore, the natural number one is the base of all cognitions for all living organisms.

   Because the natural number one is the base of all cognitions, arithmetic must absorb Euclidean geometry. For reaching this goal, we need the minimum length. Marcello Barbieri says that the brain can tell two objects apart only when their image on the retina have a distance between them of at least 0.15 mm. If we see with our eyes, 0.15 mm must be the minimum length. If we construct plane geometry based on the minimum length, the pixel or the unit square is 0.15 X 0.15 mm². Then, the width of a line is 0.15 mm and a circle is not the complete circle. This geometry is identical to the computer graphics. Moreover, the drawings of traditional paper and pencil geometry are equivalent to the figures of this geometry. In addition, the minimum length is arbitrary. If we see with the microscope, thousand-time enlargements can be obtained. Then, we can determine the minimum length under one micrometer.

   The best principle of the integration is Weierstrass's epsilon-delta definition of limit. Let us consider the simple example. The sequence a_n converges to 0:

This equation means as follows: For every ε>0, there exist an integer N>0; such that: if n>N, then 0<a_n<ε.

This principle can apply the geometry based on the minimum length. If the minimum length equals d, any a_n<d can be neglected. If we determine ε such as ε<d, then a_n=0. That is, the sequence a_n converges to 0.

In conclusion, even though Euclidean space is the imagination of our brain, epsilon-delta definition of limit is the bridge between Euclidean geometry and the geometry based on any minimum length.

Table of Contents